课题类别:华商学院校内导师制科研项目
课题名称:几类数学与管理数学的最优控制问题研究
课题批准号:2020hsds02
经费资助:12万元
项目负责人:侯春娟
论文成果名称:
1.error estimates of variational discretization for semilinear parabolic optimal control problems(sci来源期刊jcr二区,a类)
2.(山东大学学报,a类刊物)
成果简介:
1.error estimates of variational discretization for semilinear parabolic optimal control problems
主要观点:
研究带控制约束的非线性抛物型方程最优控制问题的变分离散问题。利用标准有限元的倒推欧拉法,已知其先验误差估计为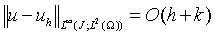 。本研究中
。本研究中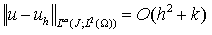
是得到的较好的结果。此外,本研究还得到了残差型的后验误差估计。
学术价值:
最优控制在工程数值模拟、经济、大气、石油、建筑和科学等不断变化的社会中有着重要的作用。同时,最优控制不仅是理工科学生的一个重要知识点,而且是非理工科学生的一个重要知识点。例如,它被广泛应用于经济管理学科,如管理会计、动态优化、精算、定价分析等,包括艺术建模的结构分析。一种有效的数值方法是最优控制成功应用的必要条件,对于最优控制问题(ocp),有限元逼近应该是一种强大的数值计算方法。
创新点:
研究了一类带控制约束的非线性抛物型方程最优控制问题的变分离散化问题,并给出了残差型的先验误差估计和后验误差估计。用变分离散法估计误差的结果是线性抛物型问题的扩展。
2.
主要观点:
研究一类带粘性项、零扩散广义boussinesq方程组局部解的存在性问题,应用正则化方法、压缩映像原理以及经典的能量估计方法,证明了带粘性项、零扩散的广义boussinesq方程组解的局部存在性,应用sobolev不等式获得解的一个爆破准则,研究结果能揭示一类特殊流体运动的物理现象ꎬ能更精确地反应流体的运动情况。
学术价值:
boussinesq方程是流体力学中一类重要的数学模型,它是流体速度与温度耦合而成的方程,是热力对流现象的一种描述,该方程不仅在大气科学中有重要应用,在海洋生态以及地球物理学中也有非常重要的作用。
创新点:
应用正则化方法,结合压缩映像原理与经典能量估计方法,得到了三维带粘性项、零扩散的分数阶boussinesq方程组解的局部存在性,应用sobolev不等式还推出了解的爆破准则,所得结果能更精确地反应
流体运动情况,在研究过程中人们发现由于大气性质的变化,中层大气中向上流动的气流发生了变化,运动扩散和热扩散的效应随大气变薄而减弱,这种反常的衰减就可以用空间分数拉普拉斯积分法来模拟,因此,在boussinesq系统中对分数耗散模型的研究有其重要的物理意义,而研究广义boussinesq系统的动机源于广义navier-stokes方程的研究。