项目研究的目的和意义
复合材料是指由两种或两种以上不同物质以不同方式组合而成的材料,在大多数情况下,它可以发挥各种材料的优点,克服单一材料的缺陷，扩大材料的应用范围。复合材料是材料领域之中的后起之秀,它的出现带来了材料领域的重大变革。鉴于复合材料应用的飞速发展,这些新材料的设计与性能评价是材料科学、计算力学等学科研究的热点。由于小周期结构的复合材料局部结构的多尺度性、多物理场的强耦合性使其在现代高新材料发展与设计中起着非常重要的作用,研究这些新型材料的等效物理、力学性能是计算材料科学、力学、计算数学等学科研究的一个新方向。本项目研究基于利用双尺度渐近展开的方法,对小周期结构复合材料建立双尺度耦合关系,在分析了均匀化常数和均匀化方程,以及均匀化方程的正则性基础上,分析了对应的双尺度解的渐近误差估计。
取得的主要成果
1.李志青,李远飞,张文彬.周期结构带阻尼项椭圆边值问题的双尺度渐近误差分析[j].海南大学学报（自科版）,2021,39(4):325-330；(cstpcd，b类)
2.石金诚.一类双曲方程解的空间渐近性态[j].高校应用数学学报a辑,2022,37(3):268-276。(cstpcd,北大核心，a类)
三、项目研究的主要内容和创新之处
（一）主要内容
1. 利用双尺度方法对周期结构带阻尼项椭圆边值问题的偏微分方程组进行了双尺度渐近展开分析，得到了对应问题的均匀化方程和均匀化常数，并分析了双尺度渐近解的误差估计.根据误差分析，得到双尺度解更加逼近于近似解的结论。
2. 研究了一类双曲方程的解的空间性态,利用能量方法与微分不等式的技巧,得到了解的类似于phragm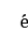
n-lindel
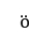f二择一定理的结果: 沿空间变量z趋于无穷大时,解或者爆破,或者衰减.接着在解衰减的基础上得到解的衰减为指数衰减,最后得到解的点点指数衰减估计。该文的结果可看成saint-venant原则在双曲方程上的应用。
（二）创新之处
1. 比较以往的研究,本论文将一个复杂的耦合微分方程组分解成两个较简单的方程组求解,另外由于该问题中涉及一些量扰动的复杂性,只能通过近似解去逼近它，目前很多文献采用双尺度方法来分析,为了提高计算的精度。本章采用双尺度分析方法,构造适当的小周期单胞函数,采用双尺度渐近误差估计提高精度。所得结论一方面为系统行为的等效性能分析提供了理论依据，另一方面为进一步进行数值计算奠定了理论基础。
2.本文讨论了解关于空间的性态,得到一个类似phragm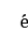n-lindel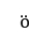f 二择一的结果。对于解的爆破现象的研究,现有文献主要集中在解的时间爆破。由于考虑对象由抛物方程变为双曲方程,如何构造能量函数是本文的关键.如何推导出能量函数所满足的微分不等式以及巧妙求解的方法,是本文最大的特色。本文所得的解的点点估计结果是双曲方程所特有的。
四、成果的应用价值
根据不同的热力耦合复合材料的结构特征,确定适当的渐近展开式和有效的双尺度方法是应用到小周期热力耦合问题的关键。随着这种方法的发展,它的应用范围在不断地扩大，在我们的计算材料，计算物理，计算力学等学科中应用很普遍，是一种高效可行的计算方法。
近几年对于一般区域中热力耦合现象的数值模拟与计算方法的讨论比较常见。而本项目则通过对具有阻尼项的强热力耦合微分方程的数值模拟及分析，分析复合材料有效物理力学性能的关键，为进一步进行数值计算奠定了理论基础。
同时phragm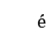
n-lindel
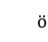f二择一原理被许多研究结果广泛推广，几类偏微分方程和系统的空间行为在近一个半世纪的文献中一直是广泛研究的课题。研究表明phragm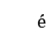n-lindel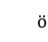f二择一原理在物理、弹性力学和流体力学等应用科学中具有重要的理论和科学意义。我们研究的是解关于空间的性态, 得到了一个类似于phragm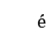n-lindel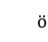f二择一的结果：沿空间变量趋于无穷大时, 解或者爆破, 或者衰减。当前研究的爆破现象主要集中在解的时间爆破, 而对空间爆破的研究极少，我们所采取的研究方法和思路为人们后续研究其他方程解的空间爆破现象提供借鉴作用。