课题类别：广东省普通高校青年创新人才项目
课题名称：迭代函数系统的伪轨跟踪性质
课题批准号：2020kqncx132
所在单位：广州华商学院数据科学学院
主要成员：李远飞、石金诚、郭连红、陈雪姣、李志青
经费：6万
一、项目研究的目的和意义
伪轨跟踪性质是动力系统中的一个重要的概念，伪轨跟踪性研究的是一个映射下的伪轨能否被真轨跟踪，最初是由bowen为了推动双曲系统稳定性理论的发展而引入的。 在动力系统的研究中，由于大部分的精确解无法得到， 学者们常用数值计算方法模拟所研究系统的轨道。 由于误差的存在，导致“伪轨”的产生。 若系统具有“通常意义下的伪轨跟踪性质”， 则对任意的一个单步误差足够小的伪轨必然被一条真轨跟踪，且其误差是一致有界的。 因此，它与系统的稳定性理论有着紧密的联系， 在动力系统的定性理论中起着重要的作用，在数值分析上也有着广泛的应用。 迭代函数（ifs）是分形理论的一个重要分支。 它是分形图像处理中最富生命力而且最具有广阔应用前景的领域之一。 迭代函数系统属于一种分形结构系统，将分形理论的精髓--自相似性， 层次多重性和不同层次的规则统一性，借助于计算机强大的迭代计算能力，引入到图像合成领域中将待生成的图像看做是由许多与整体相似的（自相似）或经过一定变换与整体相似的（自仿射）小块拼贴而成，可以产生许多具有无穷细节和精致纹理的图形。
本项目研究基于经典动力学各种伪轨跟踪性质的基础上去探讨相关经典概念引入到迭代函数系统上所能获取的一些基本性质。
通过对已经引入的一些概念，如跟踪性质，平均跟踪性质,渐近平均跟踪性质，遍历跟踪性质等去寻找更多与经典动力学有关的性状，除了上述性质以外,我们其实还可以将更多经典动力系统中的一些基本概念运用到迭代函数系统中去,如遍历性,敏感性,极小性等,从而获得更多迭代函数系统上的动力学性状。
二、取得的主要成果
1.曾鹏.平均跟踪性质的一个注记[j].高校应用数学学报a辑,
2020, v.35(04):73-80。(cstpcd,北大核心)
2.zeng, p. the asymptotic average shadowing property of iterated
function systems. bull. malays. math. sci. soc. (2021)。(sciq1）
三、项目研究的主要内容和创新之处
（一）主要内容
1.给出了平均跟踪性质的一个等价定义，并且利用该等价定义证明了:（1）如果存在一个正整数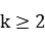
，使得
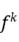有平均跟踪性质，则f也有平均跟踪性质。(2)设
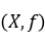是一个拓扑动力系统,如果f有遍历跟踪性质,则f有平均跟踪性质。
2.学习并研究了迭代函数系统的渐近平均跟踪性质的定义，并且证明了如果一个迭代函数系统在一定条件下具有伪轨特殊性，则它也有渐近平均跟踪性质， 从而可以得到迭代函数系统的遍历跟踪性质蕴含着渐近平均跟踪性质。 其次， 我们也证明了迭代函数系统的渐近平均跟踪性质蕴含着平均跟踪性质。最后， 我们给出了迭代函数系统中没有渐近平均跟踪性质的一个判据， 从而给出了一些迭代函数系统中不存在渐近平均跟踪性质的一些例子。
（二）创新之处
1.通过改变平均跟踪性质定义中所跟踪的伪轨，将通常意义下的平均跟踪性质定义中的平均伪轨换成遍历伪轨， 并通过研究发现该情形下所得到的定义与平均跟踪性质的概念是等价的， 并借助该定义得到了：如果存在一个正整数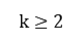
，使得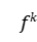
有平均跟踪性质，则f也有平均跟踪性质。其次，通过该等价定义，我们得到了遍历跟踪性质蕴含着平均跟踪性质的另外一种证明思路。
2.研究了迭代函数系统中的渐近平均跟踪性质。借助经典动力系统的相关研究方法和技术手段，并结合国内外学者的相关研究成果， 对迭代函数系统的分析方法提出了有效的改进措施。发现了在一定条件下，迭代函数系统的伪轨特殊性蕴含着渐近平均跟踪性质。其次， 我们证明了迭代函数系统的渐近平均跟踪性质蕴含着平均跟踪性质。解决了经典动力系统推广到迭代函数系统中的某些理论问题。
四、成果的应用价值
近年来，动力学的很多性状，如吸引子、极小性、传递性以及跟踪性质都可以引入到迭代函数系统中，并受到越来越多学者的青睐。基于此，更多的跟踪概念也都被推广到迭代函数系统中，如平均跟踪性质，渐近平均跟踪，遍历跟踪等，同时，动力系统的一些经典的结论也被应用到了迭代函数系统中。但是，由于迭代函数系统的复杂性，经典理论中所运用到的某些技术和方法在迭代函数系统中可能无法适用，因此，在迭代函数系统中研究跟踪性质较经典动力系统的难度更大，也更具挑战性。我们主要对迭代函数系统中的渐近平均跟踪性质，平均跟踪性质等方面做了一些突破。对迭代函数系统的分析方法做了一定的改进措施，从而获得了一些新的理论知识，为拓扑动力系统和分形理论的交叉做到了一些理论上的创新，希望后续在此基础上对该交叉领域能够开辟更多新的理论基础，从而能够得到更广阔的应用前景。